Covid19, teorÃa del caos y tecnologÃa
Mayo de 2020
De forma generalizada en muchos paÃses, hemos pasado en pocas semanas de no dar relevancia a la COVID-19 basándonos en predicciones que indicaban que se darÃan pocos casos y con poca gravedad, a darnos cuenta de que surgÃan focos de infección de forma heterogénea por paÃses, regiones y ciudades, asà como a proceder al confinamiento de la sociedad con pronósticos de contagiados, hospitalizaciones y fallecimientos que aumentaban a una velocidad sorprendente. Se han evidenciado vaivenes notables en las estimaciones publicadas por diferentes instituciones: un ejemplo notable es el del Imperial College para Reino Unido, descendiendo espectacularmente su previsión (forecast) de 500.000 a 20.000 fallecidos.
En las primeras fases de la pandemia, los modelos de predicción acerca de la evolución de la COVID-19 no han funcionado con ninguna precisión.
¿Por qué fallan tanto los modelos? ¿Estamos enfocando bien el problema? ¿En qué medida podemos apoyarnos en la tecnologÃa?
Sistemas deterministas vs. caóticos
En la tarea de pronosticar nos podemos encontrar con dos familias de sistemas a modelizar: los deterministas, que podrÃamos denominar también como estables; y los sistemas caóticos o inestables. Nos encontramos ante un ejemplo del primer grupo cuando pronosticamos dónde impactará un proyectil a partir de la dirección y velocidad a la que es disparado.
Los fÃsicos o matemáticos en estos casos reducimos el problema a una simplificación de la realidad que llamamos modelo matemático. En este caso aplicamos las leyes de la mecánica clásica de Newton[1]. Se trata de un modelo muy cercano a la realidad, estable además ante pequeñas variaciones de los inputs de dirección y velocidad de lanzamiento. Se puede incluso calcular sin más tecnologÃa que papel y lápiz. Nuestra predicción acertará con notable precisión, una y otra vez, da igual cuántas veces lo repitas. «¡Qué agradecido es un sistema determinista!», pensarán buena parte de los lectores, mayoritariamente economistas o analistas de mercados acostumbrados a ver o realizar predicciones algo menos fiables.
En el otro extremo de los sistemas se encuentra el ejemplo canónico del caos: la predicción del tiempo (weather forecast). ¿Qué tiempo hará dentro de dos semanas?
En este segundo caso el sistema real (nuestra atmósfera) es bien complejo de modelizar. Para ello es necesario contar con los valores observados de algunas de sus variables, tales como presión, humedad, temperatura y velocidad y dirección del viento con la mayor resolución espacial y temporal posible. A ellos se aplican las ecuaciones no lineales de dinámica de fluidos y termodinámica. Se trata de un sistema inestable a plazo de dÃas (efecto mariposa[2]), esto es: pequeños cambios en las condiciones iniciales pueden llevar a resultados muy diferentes. Tal es la magnitud del problema que no fue posible realizar estos cálculos con algún éxito hasta la irrupción de los ordenadores, en concreto, usando una de las primeras computadoras en 1950 -la ENIAC[3]- y el esfuerzo conjunto de un grupo de meteorólogos estadounidenses y el matemático John von Neumann.
La capacidad de cálculo es necesaria, pero por mucho que esta aumenta, la fiabilidad de los resultados choca con la naturaleza caótica del sistema, con la dificultad de poder partir de un análisis lo más cercano a la realidad (se utilizan entre otras cosas potentes algoritmos de asimilación 4D-VAR) y con el todavÃa imperfecto conocimiento de algunos procesos dinámicos y sobre todo termodinámicos. Incluso con la potencia de cálculo actual, tras setenta años del primer cálculo exitoso, solo somos capaces de obtener unas ciertas probabilidades de tiempo soleado, nublado, lluvia o nieve a plazo de dÃas o alguna semana[4].
Sistema epidemiológico
En este caso la realidad es relativamente simple de modelizar y las matemáticas involucradas para pronosticar son fácilmente entendibles. Una versión básica es el modelo SIR[5], que consiste en modelizar la dinámica de tres grupos de población que definen su acrónimo: los (S)usceptibles de infectarse, los (I)nfectados y los (R)ecuperados (e inmunes) o retirados (fallecidos). Cada individuo se asigna inicialmente a uno y solo a uno de los tres grupos. Se establecen entonces las reglas o ecuaciones de traspaso de la población de un grupo a otro y sus parámetros o inputs que son, principalmente:
- La tasa a la que los susceptibles pasan a ser infectados en un perÃodo de tiempo. Esta tasa depende de cuántos susceptibles quedan, de los infectados que hay, de la capacidad de transmisión propia de la enfermedad y de la cantidad de contactos entre infectados y susceptibles en ese perÃodo de tiempo.
- La tasa a la que los infectados se recuperan (lo relevante realmente aquà es el perÃodo de tiempo en el que pueden infectar a otros).
- Finalmente, la tasa de hospitalización y también de mortalidad en función del tipo de atención recibida.
Las matemáticas involucradas son relativamente simples y una vez que hay suficientes casos, se apoyan en la ley de los grandes números.
Veamos un ejemplo ilustrativo: Una población de cerca de cincuenta millones de habitantes, todos susceptibles de contraer una nueva enfermedad contagiosa puesto que aún no están inmunizados. Supongamos cien infectados iniciales y que cada infectado contagia, durante cinco dÃas, a dos individuos. Esto significa un «número reproductivo»o R0, de 2, que disminuirá a medida que la población vaya transitando desde susceptible a recuperada, al inmunizarse. Hasta transcurridos sesenta o setenta dÃas el impacto de los contagios no comienza a mostrar su naturaleza exponencial, pero entonces lo hace con violencia.
(millones de personas / dÃas)
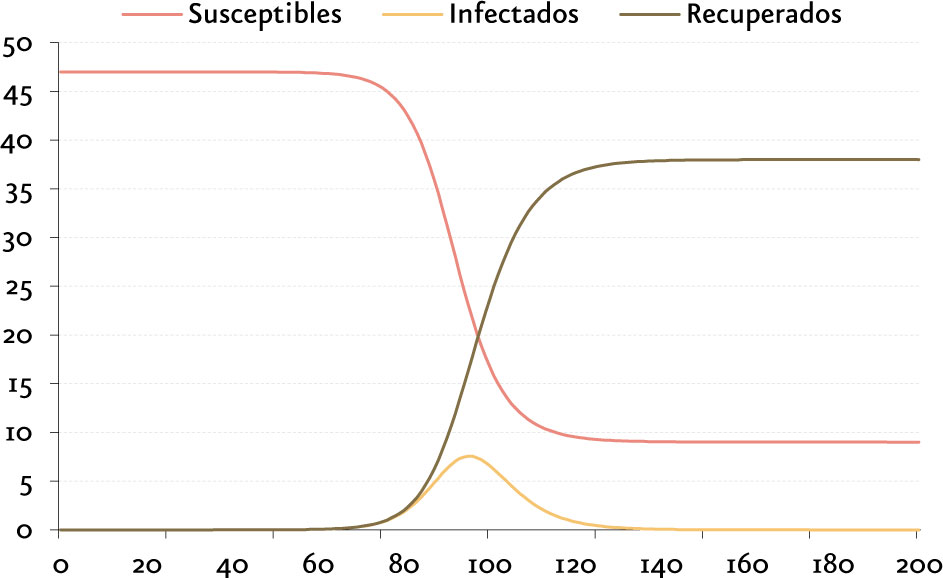
En este ejemplo el número de infectados simultáneos alcanzarÃa -en su cénit- algo más de siete millones. Supongamos también que el 1% de los infectados requieren cuidados intensivos y que en esa población hay recursos hospitalarios de ese nivel para diez mil pacientes. Si no se toma ninguna medida se habrÃa superado por mucho la capacidad del sistema sanitario.
(miles de personas / dÃas)
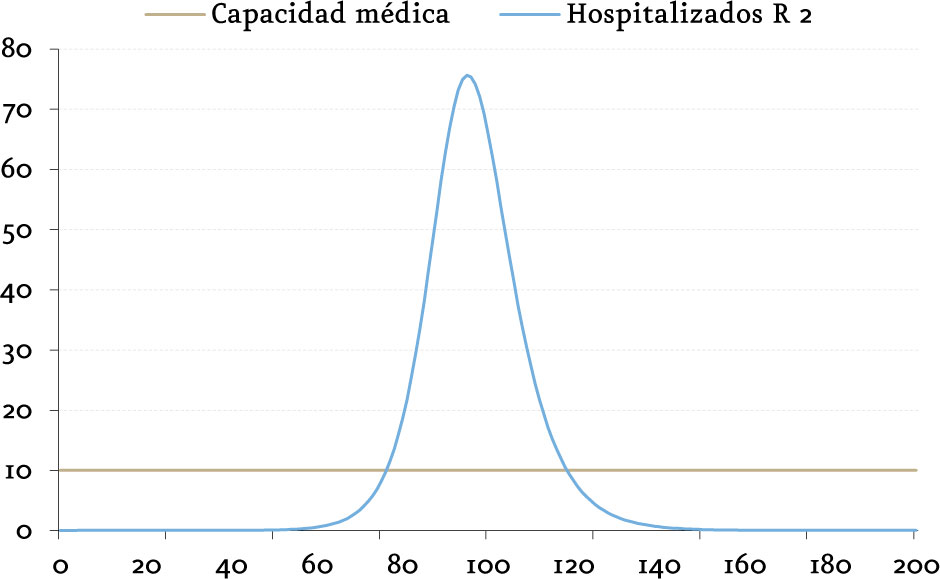
Supongamos ahora que estas predicciones alarman a las autoridades y, en el dÃa 75, ya con la capacidad sanitaria saturándose, se toman medidas de distanciamiento social que implican una rebaja en el número reproductivo desde 2 hasta 1,25. La situación cambia desde ese dÃa 75 a la mostrada las imágenes.
(millones de personas / dÃas)
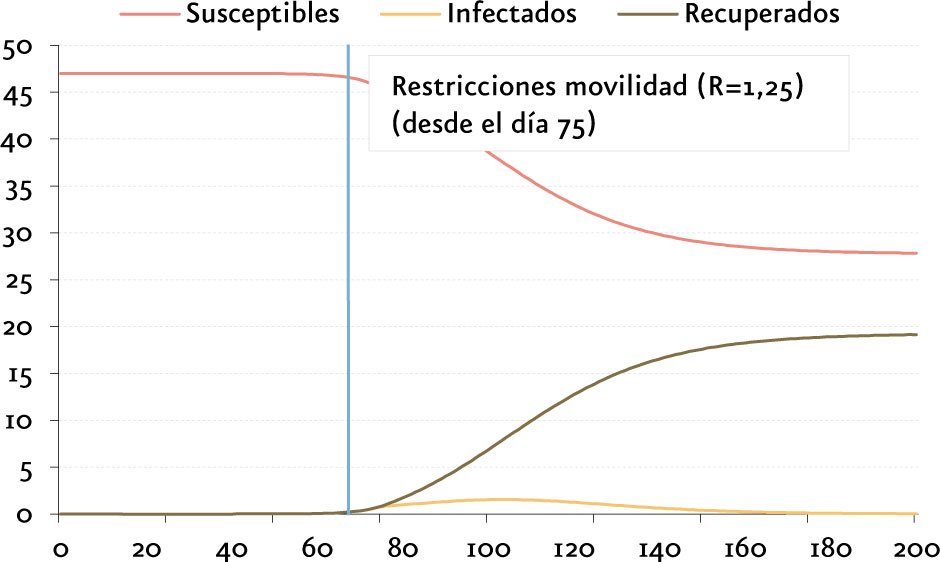
(miles de personas / dÃas)
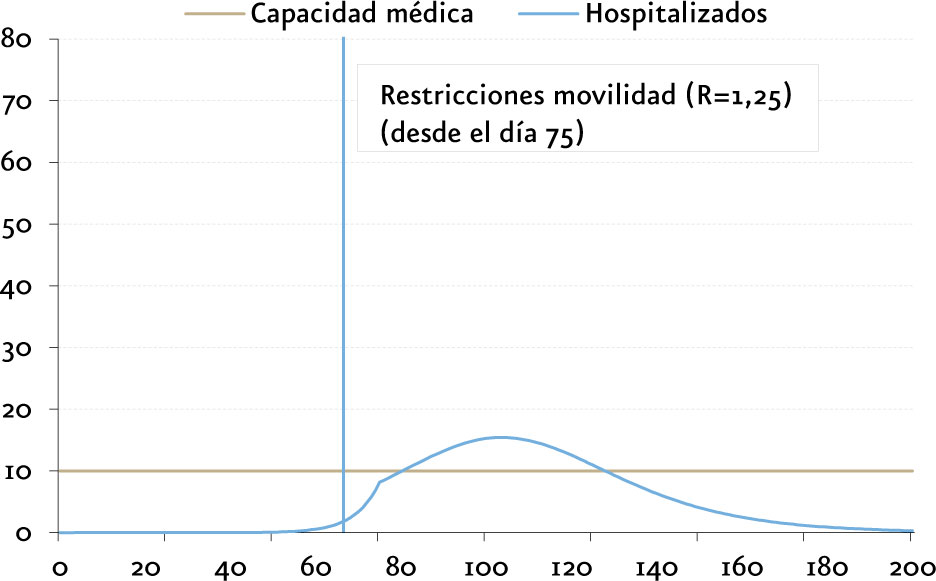
Se observa cómo las hospitalizaciones continúan aumentando, pero a un régimen no explosivo, conteniendo el problema.
En estos ejemplos hemos trabajado muy cómodamente, con unos parámetros dados, como si los conociésemos, pero la realidad no es asÃ. Cuando la enfermedad es nueva los parámetros son desconocidos. Se estiman por similitud de otras enfermedades y se van conociendo según indicadores atrasados y poco fiables (casos de contagios y decesos detectados y publicados por los gobiernos). Los casos de contagios reales pueden ser fácilmente 10 veces los detectados.
A la incertidumbre sobre la fiabilidad de los inputs se une que los resultados son muy sensibles (exponenciales) a estos parámetros, lo que nos permite clasificarlo como un sistema caótico. Se observa en la imagen la diferencia de resultados ante ligeros cambios (de 2 a 1,5) de uno de los parámetros del sistema.
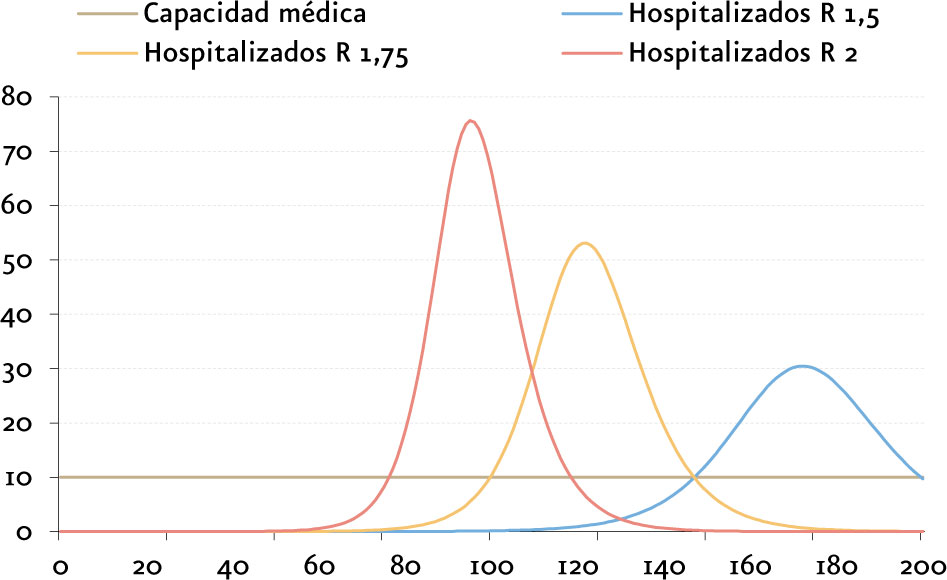
Mención especial merece el siguiente aspecto: si al efectuar las previsiones ante una nueva epidemia se toman parámetros altos, que presenten un cierto estrés, el miedo moverá a la acción, a tomar medidas en la etapa temprana de la pandemia. Precisamente esas medidas prevendrán los contagios y decesos, haciéndolos disminuir mucho sobre las predicciones. Eso es deseable, aunque se entienda que el modelo falló, alarmando, aparentemente en exceso, en el inicio de la crisis sanitaria y moviendo a los gobernantes a «desperdiciar» recursos económicos. Si, por el contrario, se efectúan previsiones con parámetros bajos, la población se protegerá tarde o muy tarde.
Forecasting vs nowcasting
Mucho antes de la irrupción de los ordenadores, en 1860, con el afán de proteger a aquellos que trabajaban en el mar, el capital Robert FitzRoy[6] lideró la fundación de la Met Office y fue el pionero de la predicción operativa y avisos, desarrollando el Storm Warning Service. Si bien las técnicas de predicción inmediata o nowcasting propiamente dichas se introdujeron en 1980 por Keith Browning, cientÃfico de la mencionada Met Office.
Son técnicas de extrapolación utilizadas para pronósticos de muy corto alcance, en ese caso observando una secuencia de imágenes de radar, satélite, descargas eléctricas y de estaciones automáticas, para anticipar, por ejemplo, el alcance y el momento del impacto inminente de eventos meteorológicos peligrosos. También se utilizan técnicas similares en terremotos y tsunamis, con predicciones inmediatas que otorgan a la población afectada segundos o minutos preciosos para protegerse del fenómeno.
Más recientemente se utiliza el término nowcasting en economÃa[7] para definir tendencias o estrategias a muy corto plazo basadas en conocimientos y hechos, como diferencial frente a las predicciones generales o forecasting.
TecnologÃa
Retomando el problema de predicciones de un sistema epidemiológico que hemos clasificado como inestable, caótico, por la incertidumbre de los inputs y el comportamiento exponencial de los contagios, ¿puede la tecnologÃa actual ayudar a convertir un problema de forecasting en otro de nowcasting?
De forma complementaria a la realización de test a la población para poder aislar los casos y reducir rápidamente el número reproductivo (R0), la tecnologÃa pone en nuestra mano capacidades para la detección temprana de infectados y de potenciales susceptibles: nuestro teléfono móvil.
Se tenga activado o no el GPS del teléfono, las compañÃas de telecomunicaciones disponen de la geolocalización de cada terminal conectado a su red. Esta información es almacenada por las compañÃas de telecomunicaciones y está a disposición de las autoridades (salvando las leyes de protección de datos[8]). Se puede inferir, utilizando técnicas de análisis de datos masivos, la probabilidad de haber sido contagiado por proximidad a algún caso confirmado o sospechoso.
Asà se ha hecho en China, informando a cada ciudadano en su teléfono móvil, eventualmente, de la obligatoriedad de aislamiento domiciliario. También se ha utilizado en Corea del Sur, remitiendo incluso a los usuarios de aplicaciones móviles diariamente los datos oficiales sobre los casos positivos en el área en el que se encuentre el usuario, permitiendo evitar los contactos esas zonas.
En Singapur se desarrolló una aplicación que, instalada en un teléfono, y mediante conectividad Bluetooth, almacena todos los números de teléfono de los terminales que han estado a menos de dos metros de proximidad durante al menos 30 minutos. AsÃ, cuando se diagnostica a alguien, se puede obtener el listado de los que han podido ser contagiados. Para facilitar y universalizar este tipo de soluciones, Apple y Google (Android) anunciaron una iniciativa conjunta para compartir esta información de contacto de Bluetooth con autoridades sanitarias a través de una API[9].
Pero no va a quedar ahà la aportación de nuestro teléfono móvil. Los cada vez más utilizados wearables prometen conseguir más. Recientemente, varias organizaciones de investigación médica[10] han lanzado nuevos esfuerzos que buscan utilizar dispositivos wearables, como relojes o anillos inteligentes para identificar o predecir la aparición de la enfermedad. Estos dispositivos son capaces de medir la actividad fÃsica por el movimiento, también el ritmo cardÃaco y ya algunos de ellos la temperatura.
Toda esta tecnologÃa, la experiencia de su uso en determinados paÃses y el impulso de organismos públicos y privados permite reducir un problema de forecasting a uno de nowcasting, mitigar el impacto de la crisis actual y seguro que afrontar la siguiente más preparados.
[1] Philosophiæ naturalis principia mathematica, Isaac Newton, 5 de julio de 1687. Recoge sus descubrimientos en mecánica, las tres leyes de la dinámica y la ley de la gravitación universal.
[2] Lorenz, E.N., 1963: Deterministic Nonperiodic Flow. J. Atmos. Sci., 20, 130-141, https://doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
[3] Electronic Numerical Integrator And Computer (Computador e Integrador Numérico Electrónico), ENIAC, fue construida en la Universidad de Pensilvania en 1946 por John Presper Eckert y John William Mauchly, ocupaba una superficie de unos 166 m² y pesaba alrededor de 30 toneladas.
[4] Agradecemos al meteorólogo del Estado, D. Ãngel Rivera Pérez, responsable de Predicción y Comunicación de la Agencia Estatal de MeteorologÃa (AEMET) entre los años 1990 y 2011, por su revisión y aportaciones técnicas a este artÃculo. Lectura recomendada: FÃsica del caos en la predicción meteorológica, editado por CARLOS SANTOS BURGUETE. Agencia Estatal de MeteorologÃa, 2018. http://www.aemet.es/es/conocermas/recursos_en_linea/publicaciones_y_estudios/publicaciones/detalles/Fisica_del_caos_en_la_predicc_meteo.
[5] A. G. McKendrick and W. O. Kermack publicaron su teorÃa en una serie de tres artÃculos en 1927, 1932 y 1933.
[6] https://www.metoffice.gov.uk/research/library-and-archive/archive-hidden-treasures/robert-fitzroy.
[7] «Nowcasting: The real-time informational content of macroeconomic data». Domenico Giannone, Lucrezia Reichlin and David Small. Journal of Monetary Economics, Volume 55, Issue 4, May 2008, Pages 665-676.
[8] Uso legÃtimo en caso de estado de alarma, como también sucede ante un requerimiento judicial. https://www.aepd.es/es/documento/2020-0017.pdf.
[9] https://www.blog.google/inside-google/company-announcements/apple-and-google-partner-covid-19-contact-tracing-technology/.
[10] https://detectstudy.org/ y https://ouraring.com/ucsf-tempredict-study.



