Black-Litterman, simbiosis entre gestor y algoritmo
Marzo de 2019
Maximizar la rentabilidad minimizando el riesgo es un objetivo clásico en la gestión de carteras. Mediante diferentes técnicas se buscan los activos y ponderaciones óptimos que consigan un mix apropiado de ambas medidas para cada perfil de inversor (búsqueda de rentabilidad vs. tolerancia o apetito al riesgo).
Sobre la base de la optimización de carteras clásica rentabilidad-riesgo de Markowitz han surgido otros algoritmos o entornos que buscan solventar algunas deficiencias o añadir valor al proceso. Algunos de los problemas que la experiencia ha aflorado son:
- Inestabilidad del resultado de cartera propuesta: Esto es, que un algoritmo sugiera una composición de cartera hoy, pero el mismo algoritmo sugiera una muy diferente la próxima semana.
- Dependencia de la historia: Resultados pasados no presuponen comportamientos futuros, tanto en rentabilidad como en volatilidad o en correlación.
- Dependencia de opinión de expertos analistas: Son buenos, pero somos conscientes de que no son infalibles.
Una de las soluciones es el entorno de optimización de carteras de Black-Litterman (propuesto por Fischer Black y Robert Litterman en la década de los 90 del s. XX), que representa una combinación estratégica entre conocimiento de analistas y algoritmo matemático.
Black-Litterman permite incluir en la optimización no sólo opiniones sino también cómo de seguros estamos de esas opiniones. Éste es un avance muy significativo frente a los algoritmos clásicos de optimización de carteras.
Este algoritmo abre las puertas a una interacción entre el gestor -conocedor del mercado y sus tendencias- y la máquina -portadora de la formulación que conjuga las informaciones para proveer al gestor de la cartera óptima. En este sentido, ambas partes intervinientes se nutren mutuamente en pro de la creación y gestión de una cartera óptima que refleje el conocimiento y pericia de ambos. ¿Es un principio de evolución hacia un aprendizaje iterativo hombre-máquina? En nuestra opinión, claramente sÃ.
En la literatura sobre este modelo se puede encontrar multitud de versiones sobre la original que, o bien no están debidamente definidas, o bien se prestan demasiado a la interpretación del lector. Una simple búsqueda en nuestro navegador favorito puede dar fe de esta diversidad.
En todo caso, en este marco Black-Litterman el gestor opina sobre las rentabilidades futuras de cada activo y da una confianza entre 0-100% sobre cada opinión, pudiendo dejar de opinar sobre algunos activos. En principio se pueden incluir tantas opiniones como se quiera, siempre que se tenga cuidado con la aparición de inconsistencias. Estas opiniones pueden ser de dos tipos:
- Opiniones relativas: «El activo A tendrá una rentabilidad un 2% superior a la rentabilidad del activo B con una seguridad del 70%».
- Opiniones absolutas: «El activo A tendrá una rentabilidad de 5% con una seguridad del 80%».
Además, al tratarse en última instancia de un proceso de optimización matemática, el gestor puede añadir restricciones derivadas de la estrategia que se persiga o las polÃticas que limiten la actuación, como son:
- Restricción al nivel de riesgo, o volatilidad de la cartera total: «La volatilidad de la cartera no puede ser superior al 15%».
- Restricción al peso por activo: «El peso que se le asigne al activo A no puede ser inferior a un 20% ni superior a un 40%».
- Restricción al peso relativo de los activos: «El peso que se asigne al activo A no puede ser superior al que se asigne al activo B».
(%)
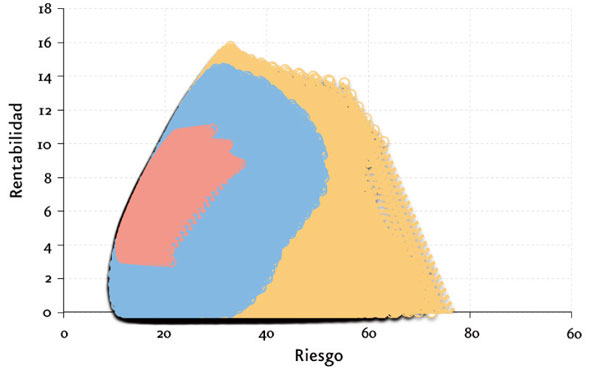
El algoritmo implica un procesado previo de los datos uniendo la teorÃa clásica de Bayes con una apropiada estructuración algebraica. Este tratamiento da robustez a los datos y disminuye su sensibilidad a posibles errores de coherencia inherentes en la optimización clásica del binomio rentabilidad-riesgo. Evita la aparición de carteras extremas para dar paso a carteras más intuitivas y cuyos resultados son mucho más aceptables frente a, por ejemplo, los obtenidos por la pura metodologÃa de Markowitz.
AsÃ, los pesos obtenidos presentan un desplazamiento consistente respecto del equilibrio de mercado, pero que pueden no ser despreciables respecto a ese equilibrio si asà lo fuerzan las opiniones y parámetros considerados (como la matriz de correlaciones, engranaje principal del algoritmo). Nótese en este sentido que opiniones muy disruptivas y con alta confianza respecto del consenso de mercado y/o una matriz de correlación muy estresada pueden forzar a que la solución diste mucho de una, a priori, frontera eficiente.
Si lo analizamos más allá, en términos de riesgo, la metodologÃa seguida por el algoritmo es lógica, ya que, si hay incertidumbre acerca de la información que se maneja, se penaliza con una valoración de más riesgo.
Entre las crÃticas al algoritmo, cabe destacar quizás el supuesto de distribuciones de rentabilidad normales. En este sentido, existe ya una generalización desarrollada e introducida por Meucci en 2008[1] que permite deformar la distribución inicial y dar opiniones mucho más generales.
También se apunta en ocasiones una sensación de dificultad de definición de parámetros y de interpretación de los resultados. Estamos de acuerdo, no es un entorno simple y exige conocimientos y rodaje, pero estamos convencidos desde la experiencia de su utilidad.
Recapitulando...
¿Se vislumbra un futuro de gestión de carteras basado en este entorno de algoritmos? No cabe duda de que Black-Litterman tiene un hueco para avanzar de la mano del gestor en una relación de beneficio mutuo, en la que el gestor le aporta a la máquina de cálculo el conocimiento de los mercados que no tiene y la máquina le indicará como actuar en base a esas opiniones y le alertará en caso de que sean inconsistentes o carentes de coherencia.
Pudiera parecer que el término simbiosis trasciende en este caso a su origen puramente biológico (como asociación Ãntima de organismos de diferentes especies para beneficiarse mutuamente en su desarrollo vital) y podrÃa aplicarse a la relación hombre-máquina subyacente en el entorno de algoritmos de Black-Litterman.
[1] Meucci, A.: «Beyond Black-Litterman: Views on Non-Normal Markets». Risk 19 (2006), 2,96-102. Meucci, A.: «The Black-Litterman Approach: Original Model and Extensions». Working paper, www.symmys.com, 2008. .
 Raquel Hernández es consultora del área de Finanzas Cuantitativas de Afi.
Raquel Hernández es consultora del área de Finanzas Cuantitativas de Afi.

